$\sf\large\text{Size Balanced Tree}$(节点大小平衡树,下简称SBT)是陈启峰在WC2007提出的一种新型平衡树。
SBT的高度为log n,其核心操作maintain()复杂度O(1),其他操作均为O(log n),所以是平衡树中非常优秀的一种。其主要通过子树大小来维持其平衡性质。
和其他平衡树一样,SBT支持大部分较为常规的操作:
1
2
3
4
5
6
7
| insert(x,val):向x子树插入值为val的结点
del(x,val):删除x子树中值为val的结点
find(x,val):查找x子树中值为val的结点
rank(x,val):返回x子树中val的排名
kth(x,k):返回x子树中排名第k的结点(大小排序均可)
pre(x,val):返回x子树中val的前驱
suc(x,val):返回x子树中val的后继
|
$\sf\large\text{1.SBT的结点定义}$
1
2
3
4
5
6
7
8
9
10
| #define ls(x) t[x].l
#define rs(x) t[x].r
struct SBT
{
int l;
int r;
int val;
int siz;
}t[maxn];
|
SBT有一个特殊的性质需要维护:某子树的大小大于等于其兄弟子树的大小。
直观写出来就是:
1
2
| t[ls(i)].siz>=max(t[rs(rs(x))].siz,t[ls(rs(x))].siz);
t[rs(i)].siz>=max(t[ls(ls(x))].siz,t[rs(ls(x))].siz);
|
$\sf\large\text{2.SBT的左右旋}$
SBT也是需要旋转的,且同样分为左右旋两种。
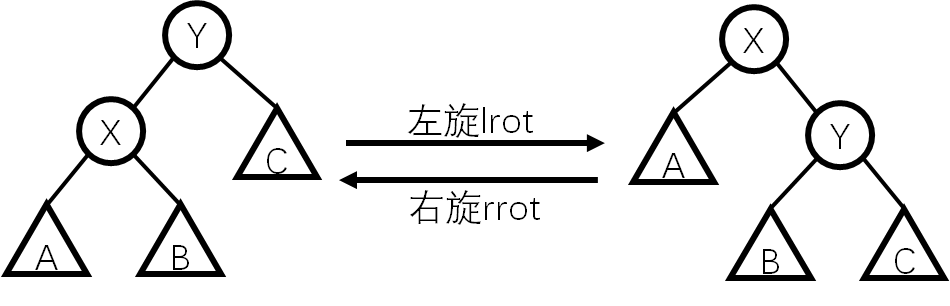
我们列出旋转前后的状态,即
1
2
3
4
5
6
7
8
9
10
11
12
13
| 左旋前:
根:rt 左子树的根:L
右子树的根:R_rt 右子树的子树:R_l,R_r
左旋后:
根:R_rt 右子树的根:R_r
左子树的根:rt 左子树的子树:L,R_l
右旋前:
根:rt 右子树的根:R
左子树的根:L_rt 右子树的子树:L_l,L_r
右旋后:
根:L_rt 左子树的根:L_l
右子树的根:rt 右子树的子树:L_r,R
|
左右旋代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| void lrot(int &x)
{
int y=rs(x);
rs(x)=ls(y);
ls(y)=x;
t[y].siz=t[x].siz;
t[x].siz=t[ls(x)].siz+t[rs(x)].siz+1;
x=y;
}
void rrot(int &x)
{
int y=ls(x);
ls(x)=rs(y);
rs(y)=x;
t[y].siz=t[x].siz;
t[x].siz=t[ls(x)].siz+t[rs(x)].siz+1;
x=y;
}
|
$\sf\large\text{3.SBT的维护}$
首先,假设一株满足条件的SBT长这样:
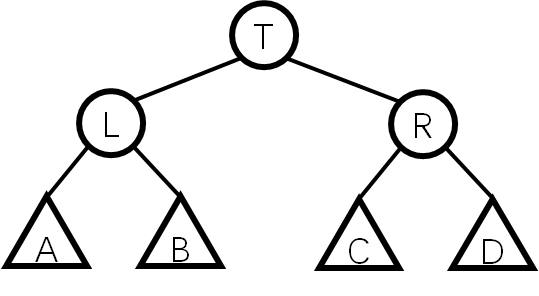
此时有A.siz,B.siz≤R.siz并且C.siz,D.siz≤L.siz
每当插入一个值的时候,平衡树的平衡性就可能被打破,所以我们要使用O(1)的maintain(x)对x子树进行修复操作。
插入后,可能会出现以下的四种情况:
1
2
3
4
| * t[ls(ls(x))].siz>t[rs(x)].siz
* t[ls(rs(x))].siz>t[rs(x)].siz
* t[rs(rs(x))].siz>t[ls(x)].siz
* t[rs(ls(x))].siz>t[ls(x)].siz
|
直接分类处理会很复杂。但SBT的对称性质使我们只用讨论两种情况:
$\sf 1.t[ls(ls(x))].siz>t[rs(x)].siz$
看到上图,对于T子树,此时的情况就是A.siz>R.siz,显然此时就导致平衡性质受损。
第一步,我们先将其右旋,得到下面这株可能仍然不满足性质的树:
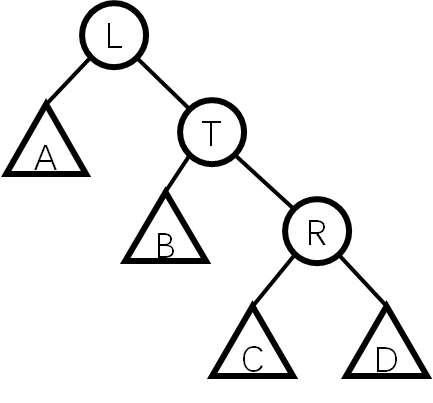
之所以说可能仍不满足性质,是因为C.siz>B.siz或D.siz>B.siz的情况可能发生,所以有必要再次使用maintain(T)。这样一来,L的右子树就会被多次调整,不过别担心,每次调整都是O(1)的。
$\sf 1.t[rs(ls(x))].siz>t[rs(x)].siz$
(为了直观,此处增加结点数)上述情况在下图中表示为:B.siz>R.siz
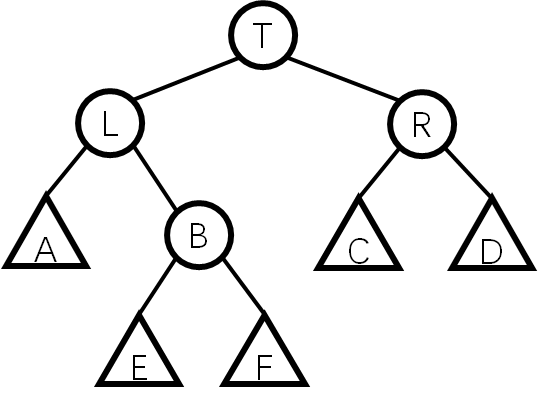
那么对称地,我们先进行左旋,得到:
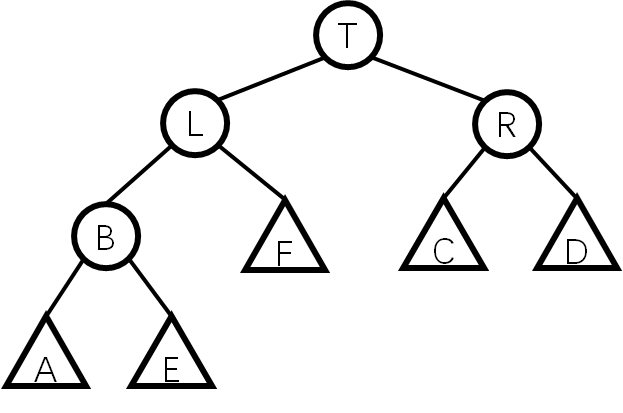
不同的是,接下来我们还要进行一次右旋,得到:
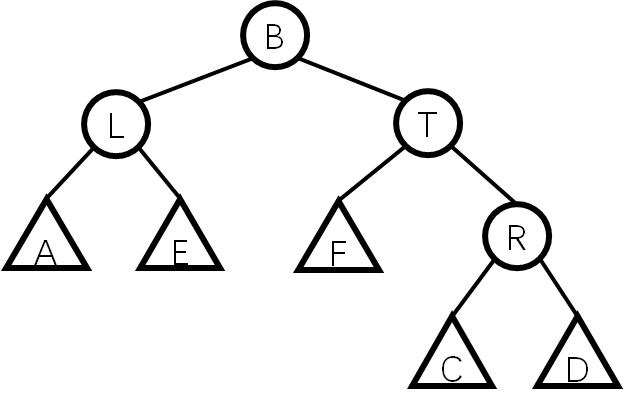
有同学可能就会问了:左旋右旋过后这棵树就很不稳定了,怎么办?
答:没事,至少图中的小子树还是满足性质的,所以只要maintain一下L和T就可以让L,T子树平衡。最后再来一次maintain(B)即可。
情况3,4与上述两种情况分别相反,对应操作即可,此处不再赘述。
maintain采用递归实现,具有一定的对称美感。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| void maintain(int &x,bool lr)
{
if(lr)
{
if(t[ls(ls(x))].siz>t[rs(x)].siz)
{
rrot(x);
}
else if(t[rs(ls(x))].siz>t[rs(x)].siz)
{
lrot(ls(x));
rrot(x);
}
else
{
return ;
}
}
else
{
if(t[rs(rs(x))].siz>t[ls(x)].siz)
{
lrot(x);
}
else if(t[ls(rs(x))].siz>t[ls(x)].siz)
{
rrot(rs(x));
lrot(x);
}
else
{
return ;
}
}
maintain(ls(x),1);
maintain(rs(x),0);
maintain(x,0);
maintain(x,1);
}
|
$\sf\large\text{4.插入元素}$
SBT的插入和其他平衡树基本一致,只是向非空子树插入元素时要maintain一下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void insert(int &x,int val)
{
if(x==0)
{
x=++cnt;
ls(x)=rs(x)=0;
t[x].siz=1;
t[x].val=val;
}
else
{
t[x].siz++;
if(val<t[x].val)
{
insert(ls(x),val);
}
else
{
insert(rs(x),val);
}
maintain(x,val<t[x].val);
}
}
|
$\sf\large\text{5.查找前驱&后继}$
查找前驱函数pre(),我们传入三个参数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int pre(int &x,int p,int val)
{
if(!x)
{
return p;
}
if(t[x].val>=val)
{
return pre(ls(x),p,val);
}
else
{
return pre(rs(x),x,val);
}
}
|
后继同理:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int suc(int &x,int p,int val)
{
if(!x)
{
return p;
}
if(t[x].val>val)
{
return suc(ls(x),x,val);
}
else
{
return suc(rs(x),p,val);
}
}
|
$\sf\large\text{6.删除元素}$
删除元素的操作与BST的删除基本一致。删除之后maintain也是没有必要的,其原因是:
虽然不能保证删完后还是SBT,但是树的最大深度不会变化,时间复杂度也并不变化,maintain就显得多余了。
删除有两种主流方法,均可使用:
1.后继替换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| int del(int &x,int val)
{
t[x].siz--;
if(val>t[x].val)
{
del(rs(x),val);
return ;
}
else if(val<t[x].val)
{
del(ls(x),val);
return ;
}
if(ls(x)&&!rs(x))
{
int reg=x;
x=ls(x);
return reg;
}
else if(!ls(x)&&rs(x))
{
int reg=x;
x=rs(x);
return reg;
}
else if(!ls(x)&&!rs(x))
{
int reg=x;
x=0;
return reg;
}
else
{
int reg=rs(x);
while(ls(res))
{
reg=ls(reg);
}
t[x].val=t[reg].val;
del(rs(x),t[reg].val);
}
}
|
2.前驱替换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int del(int &x,int val)
{
int reg;
t[x].size--;
if((val==t[x].val)||(val<t[x].val&&!ls(x))||(val>t[x].val&&!rs(x)))
{
reg=t[x].val;
if(ls(x)&&rs(x))
{
t[x].val=del(ls(x),t[x].val+1);
}
else
{
x=ls(x)+rs(x);
}
}
else if(val>t[x].val)
{
reg=del(rs(x),val);
}
else if(val<t[x].val)
{
reg=del(ls(x),val);
}
return reg;
}
|
$\sf\large\text{7.一系列的查询操作}$
1.最值查询(单向爬树)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int extremum(int x,bool minmax)
{
if(minmax)
{
while(ls(x))
{
x=ls(x);
}
}
else
{
while(rs(x))
{
x=rs(x);
}
}
return t[x].val;
}
|
2.查询第k小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int kth(int &x,int k)
{
int cur=t[ls(x)].siz+1;
if(cur==k)
{
return t[x].val;
}
else if(cur>k)
{
return kth(ls(x),k);
}
else
{
return kth(rs(x),k-cur);
}
}
|
若要查询第k大,则对几个选择结构中的内容进行交换并调整即可。
3.查找排名
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int rank(int &x,int val)
{
if(val==t[x].val)
{
return t[ls(x)].siz+1;
}
else if(val<t[x].val)
{
return rank(ls(x),val);
}
else
{
rank(rs(x),val)+t[ls(x)].siz+1;
}
}
|
关于树高log n的证明以及maintain时间复杂度O(1)的证明,陈启峰在论文中有提到,详见此处。
最后,以LuoGu3369作为例题,SBT的代码实现见此,用时142ms,已经算是很优秀的平衡树了。





